综述

本文主要介绍图的基本算法，包括图的表示、深度优先搜索和广度优先搜索、拓扑排序以及强连通分量等。本文的完整代码可以在我的github找到。

图的表示

图为定点和边的结合，常用图G=(V, E)来标记。图有两种常见的表示方法：邻接链表法和邻接矩阵法。邻接链表法记录一个数组Adj，数组的大小为|V|，数组的每个元素Adj[u]为一个链表，链表指向以u为起点的边。邻接矩阵法使用一个二维数组Adj来表示图，数组的维度为$|V|^2$，数组中的元素Adj[u][v]表示是否存在从u到v的边。图可以分为有向图和无向图。当一条边存在于无向图中，则其反向边也存在于无向图中，有向图则不一定。

对于权重图，邻接链接法只需在链表的结点出增加一个权重属性，邻接矩阵法则在相应的边上存放相应的权重，如果该边不存在，用0或者$\infty$表示。邻接链表法表示的图其python代码示例如下：

INF = float('inf')

class Node:
    def __init__(self, v, w):
        self.v = v
        self.w = w
        self.pre = None
        self.next = None


class LinkGraph:
    def __init__(self, n):
        self.n = n
        self.adj = n * [None]

广度优先搜索

对于图G=(V, E)，广度优先搜索从一个源结点s出发，系统性地遍历所有s能到达的结点。记$d[v]$为从源结点s到v所经历的最短边。在广度优先搜索总是先遍历$d[v]=k$的边，再遍历$d[v]=k+1$的边。广度优先搜索的python代码示例如下：

def bfs(self, s):
    d = self.n * [INF]
    color = self.n * ['white']
    parent = self.n * [None]
    d[s] = 0
    color[s] = 'gray'
    queue = [s]
    while queue:
        u = queue.pop(0)
        node = self.adj[u]
        while node:
            v = node.v
            if color[v] == 'white':
                color[v] = 'gray'
                d[v] = d[u] + 1
                parent[v] = u
                queue.append(v)

            node = node.next

        color[u] = 'black'


    return parent

广度优先搜索使用一个先进先出的队列，此处使用python的列表作为队列使用。此处的广度优先搜索记录了从源结点s到v所经历的边数d[v]、v的前驱结点parent[v]。color[v]是为了避免重复访问某结点而是设置的状态数组。如果color[v]为白色，则结点v尚未被访问；如果color[v]为灰色，则结点v已经被访问，而结点v的邻接结点尚未访问完；如果color[v]为黑色，则结点v的邻接结点已经被访问完。实际上，如果没有特殊的要求，我们只需要两个状态就可以进行广度优先搜索，即黑和白。此是我们可以用一个bool数组flar[v]保存状态，初始时均为False，当访问到结点v，即将其设为True。

对于图G=(V, E)和源结点s，我们定义图G的前驱子图为

$$G_\pi=(V_\pi, E_\pi), V_\pi=\lbrace v\in V:v.\pi \neq NIL \rbrace \bigcup\lbrace s \rbrace, E_\pi=\lbrace (v.\pi, v): v\in V -\lbrace s \rbrace\rbrace$$

如果$V_{\pi}$由从源结点s可以到达的结点组成，且对于所有$v\in V_\pi$，子图$G_\pi$包含一条从s到v的简单路径（不成环），且该路径为图G从s到v的最短路径（边最少），则前驱子图$G_\pi$为一棵广度优先树。

广度优先搜索的parent数组所得到前驱子图即为一棵广度优先树。下图为一个无向图。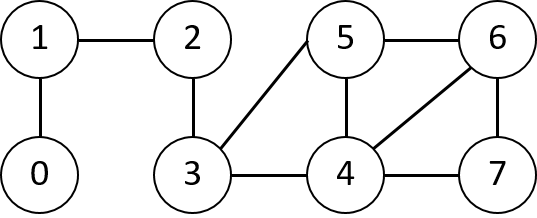

从源结点2出发进行广度优先搜索，即可得到广度优先树中的所有边，也称为树边。我们将s=2到所有结点的路径打印如下：

2 to 0: 2->1->0
2 to 1: 2->1
2 to 3: 2->3
2 to 4: 2->3->4
2 to 5: 2->3->5
2 to 6: 2->3->5->6
2 to 7: 2->3->4->7

深度优先搜索

深度优先搜索，故名思义，总是尽可能往图的深处进行搜索。深度优先搜索的前驱子图形成一个由多棵深度优先树构成的深度优先森林。如果广度优先树，每一棵深度优先树的边也称为树边。其python代码实已如下：

def dfs_visit(self, u, color, parent, d, f, time):
    time[0] += 1
    d[u] = time[0]
    color[u] = 'gray'
    cur = self.adj[u]
    while cur:
        v = cur.v
        if color[v] == 'white':
            parent[v] = u
            self.dfs_visit(v, color, parent, d, f, time)
        cur = cur.next
    time[0] += 1
    f[u] = time[0]
    color[u] = 'black'
def dfs(self):
    color = self.n * ['white']
    parent = self.n * [None]
    d = self.n * [-1]
    f = self.n * [-1]
    time = [0]
    for u in range(self.n):
        if color[u] == 'white':
            self.dfs_visit(u, color, parent, d, f, time)

    return d, f, parent

深度优先搜索中d记录除此到达的时间实际上也为广度有效搜索的最短路径，记录完成时间，即对v完成深度优先搜索时的时间。color也可以如广度优先搜索只用两种状态来表示。为了将time作为引用传递，将time设为数组。对一个结点进行深度优先搜索，可以用dfs_visit过程。

上述使用三种状态的颜色，其实并非完全没有作用。有以下引理

一个有向图G是无环的当且仅当对其的深度优先搜索不产生后向边。

对图G深度优先搜索得到的深度优先森林$G_\pi$，有以下四种边的定义：

树边：深度优先森林$G_\pi$的边。如果结点v是因算法对边的探索而首先被发现，则(u, v)是一条树边
后向边：结点u连接在其在深度优先树中的一个祖先结点v的边，自循环也是后向边。
前向边：是结点u连接在其在深度优先树中一个后代结点v的边(u, v)。
横向边：除上述边之外的所有的边。只要一个结点不是另一个结点的祖先。

在深度优先搜索中可以根据保存的数组信息，判断边的类型。当第一次访问边(u, v)时，结点v的颜色可以帮助我们判别

结点v的颜色为白色，则表明(u, v)时树边
结点v为灰色，边(u, v)为后向边
结点v为黑色，边(u, v)为前向边或者横向边。

当结点v为黑色时，如何判断横向边或者前向边，可以借助d和f两个数组。首先引入括号化定理：

对于有向图或无向图进行深度优先搜索时，对于任意的两个结点u和v，以下三种情况只有一种成立：

[u.d, u.f]和[v.d, v.f]完全分离，u不为v的后代， v不为u的后代

[u.d, u.f]完全包含在[v.d, v.f]内，则u为v的后代。

[v.d, v.f]完全包含在[u.d, u.f]内，则v为u的后代。

上数三种情况有且仅有一种成立。因此，可以据此证明当结点v为黑色时，如果过u.d < v.d，则(u, v)为前向边；当u.d > v.d时，为横向边。当u.d < v.d时，因为u.f > v.f ，则根据括号化定理，则u为v的祖先。否则，v.d < u.d, 然而v.f < u.f, 则 [u.d, u.f]和[v.d, v.f]完全分离，u和v不是祖先和后代的关系。

拓扑排序

对于有向无环图G=(V, E)，拓扑排序是所有结点的一种线性次序，该次序满足以下条件：如果图包含边(u, v)，则结点u在拓扑排序中排在v的前面。拓扑排序基本思路很简单，就是对树进行深度优先搜索，每个结点的搜索完成时，将其插入到链表的头部。其python代码示例如下：

def topo_sort(self):
_, f, _, = self.dfs()
d = []
for v, k in enumerate(f):
    d.append((k, v))

d = sorted(d, key=lambda x: x[0], reverse=True)
for item in d:
    print(item[1])

这里直接调用dfs，得到其完成时间的数组f，对数组f进行降序排序，即可得到其拓扑排序。

强连通分量

对于有向图G=(V, E)的强连通分量是一个最大结点结合$c \subseteq V$, 对于该集合的任意一对结点u和v，u和v可以互相到达。求解强连通分量的基本依据为：图G中的强连通分量和图G的转置$G^T$完全相同。$G^T$即为将图G中的边全部反向得到的图。其python代码示例如下：

def reverse(self):
    g = LinkGraph(self.n)
    for i in range(self.n):
        cur = self.adj[i]
        while cur:
            v = cur.v
            g.insert(v, i, 1)
            cur = cur.next
    
    return g

def scc(self):
    g = self.reverse()
    flag = g.n * [False]
    q = []
    for u in range(g.n):
        if not flag[u]:
            g.dfs_scc(u, flag, -1, q=q)

    count = 0
    flag = self.n * [False]
    com = self.n * [-1]
    for u in q:
        if not flag[u]:
            self.dfs_scc(u, flag, count, com)
            count += 1

    return com

def dfs_scc(self, u, flag, count, com=None, q=None):
    flag[u] = True
    if com:
        com[u] = count
    cur = self.adj[u]
    while cur:
        v = cur.v
        if not flag[v]:
            self.dfs_scc(v, flag, count, com, q)
        cur = cur.next
    if q is not None:
        q.insert(0, u)

强连通分量并不复杂，上面的代码基本思路如下：

求解图G的转置图$G^T$。
对$G^T$进行深度优先搜索，根据结点完成时间降序排列，对图G进行深度优先搜索，并得到每一个结点对应的分量。

可以看到dfs_scc和dfs_visit基本一致，只不过我们根据我们的目的做了微小的改动。我们并没有保存完成时间，而是当结点完成后，将其插入在列表q的前面，从而得到按照完成时间降序排列的结点集，然后对图G进行深度优先搜索，在深度优先搜索的过程中，为每个结点赋予其分量的编号。如果$com[i]=j$在第i个结点在第j个强连通分量上。从一个连通分量上的任意一个结点出发，该连通分量的所有点都将被访问，flag设置为True。因此，进入几次dfs_scc函数，有几个强连通分量。

如果将强连通分量视为一个结点，则有强连通分量构成的图必定为有向无环图。在进行第二次深度优先搜索（即对图G进行深度优先搜索）时，按照$G^T$深度优先搜索的完成时间进行遍历的原因可见下面的图解。

假设图G中存在两个强连通分量A, B，且这两个强连通分量有边相连，则从A到B的所有边的方向必然一致。如果不一致，则A, B为同一个强连通分量，与假设不符。不失一般性，我们只画出强连通分量的之间的一条边。如下图所示：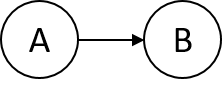

因为从A到B有一条有向边，则强连通分量A中的所有结点的完成时间都大于强连通分量B中的完成时间。则如果按照完成时间降序对$G^T$进行深度优先搜索，则必然先对强连通分量A中的结点进行深度优先搜索。$G^T$如下图所示：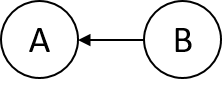

若先对强连通分量A中的结点进行深度优先搜索，则B中的结点一定不会被所引索引到，从而将不同的强连通分量隔离开。当然，先对图G进行搜索还是先对
图$G^T$进行搜索结果都是一样的。

假设原来的图G如下：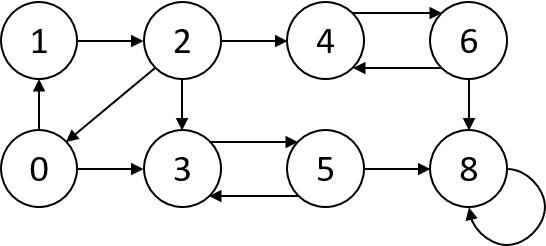

则其强连通分量的输出结果com如下：

Reference

本文主要参考《算法导论》。